Nella presente lezione, si va ad analizzare un approccio semplificato per la soluzione di problemi assial simmetrici, quali forzamenti albero mozzo, tubi etc. con caricamenti uniformi anch'essi assial simmetrici. Si consideri un elemento 4 nodi assialsimmetrico piano, quindi in condizione di tensione e deformazione piana,rappresentante una sezione di un solido di rivoluzione, con caricamento, assialsimmetrico, cioè avente carichi uguali per ogni angolo di rivoluzione.
Nel manipolatore Marc, il quadrilatero deve essere considerato accoppiato, all'asse di rivoluzoine, nello specifico si consideri l'asse x, con y=0 e z=0.
Fisicamente si andrà a disegnare l'elemento per coordinate nodali sul piano xy, con z uscente, successivamente da unire tra loro, implicitamente così facendo si è modellato un anello di rivoluzione definito dal quadrilatero stesso e dall'asse.
Gli spostamenti nodali sono 2, uniformandosi al sistema cilindrico standard, si avrà:
- u spostamento radiale
- w spostamento assiale
Spostamenti e forze applicate sui singoli nodi, sono da considerarsi distribuiti e applicati sulla circonferenza ottenuta dalla rivoluzione, si avrà dunque una forza distribuita e non nodale,
pari ad una forza per unità di lunghezza moltiplicata per la lunghezza della circonferenza 2πR, di conseguenza carichi uniformi sono rappresentabili con forze nodali linearmente crescenti in R (img. 1 e 2)
Valutando in via esemplificativa un tubo, sempre in ipotesi di caricamento assial simmetrico, si può dimostrare che ogni piano diametrale rappresenti un piano, di simmetria, risulta dunque lecito valutare porzioni sempre più piccole, ottenute mediante i suddetti piani, che possono degenerare fino all'infinitesimo (img.3)

Il numero di gradi di libertà dell'elemento a 4 nodi, nel piano si riduce ad uno, infatti l'unico spostamento che coincide con un moto di corpo rigido, risulta essere la traslazione in direzione assiale, al quale non è associata energia potenziale elastica. Viceversa i moti radiale e di rotazione inducono stiramento delle fibre dunque necessitano di forza finita per essere generati, come da figura.

La definizione di caricamento elastoplastico e l'analisi dei caricametni non asialsimmetrici, viene analizzata in appendice.
Modellazione elastica
Costruiamo la mesh di un tubo assialsimmetrico. Creiamo la fettina da 1 mm e da 100 mm, i punti e nodi di riferimento. Clicchiamo in sequenza i seguenti pulsanti: mesh generation, pts, add, scriviamo sulla riga di comando in basso le coordinate degli estremi del segmento associato all’asse di simmetria:
x,y,z
0,0,0
1,0,0
Ora mettiamo direttamente i nodi e non i punti: Mesh generation, node, add, poi inserisco da tastiera i valori che voglio:
x, y,z
0,10,0
0,20,0
1,10,0
1,20,0
n.b. non ha senso fisico caricare i nodi che giacciono sull'asse di assialsimmetria, in quanto simulano un corpo pieno.
Ora creiamo un cubo ad 1 mm di distanza, aggiungiamo un punto in 2,0,0 e proviamo a mettere un altro punto in 102,0,0 ma è troppo lontano, lo eliminiamo facendo undo, metto un punto in 42,0,0.
Ora aggiungiamo i nodi analoghi: mesh generation nodes add:
2,10,0
2,20,0
42,10,0
42,20,0
Stessa cosa con quota x =42.
Ora creiamo i due elementi quadrilateri, uno sulla prima fetta, uno sulla seconda, giunti a questo punto facciamo mesh generation, elements, add, col mouse selezioniamo il nodo 0,10,0 poi andando in verso antiorario selezioniamo anche gli altri che troviamo fino a formare un rettangolo; cosi anche per l'altra figura (se partiamo da un nodo diverso cambiano i comandi successivi di suddivisione perchè relativi agli assi, se andiamo in verso orario ci da errore perché troviamo uno Jacobiano negativo e anche l'area), il primo lato è evidenziato con una freccia.
Abbiamo il volume del materiale elastico.
Ora suddividiamo i nostri elementi: parto da quello più grande, mesh generation subdivide, possiamo dividere elementi già piazzati in particolare nella condizione di default sono definite il numero di divisioni, 2 sul primo, secondo e terzo asse. Sempre nella tendina di subdivide abbiamo un menu bias factors che sono deviazioni dall'equidistanziato, non li usiamo, 0,0,0 vuol dire divisione equidistanziati su tutti e tre gli assi. Facciamo 1 elemento ogni mm, quindi inseriamo i valori: 40, invio, 10, invio, e 1 (suddivisione sul terzo asse ), invio.
Definiti i paramentri della suddivisione li applichiamo all'elemento: clicchiamo su elements e selezioniamo l'elemento da dividere cliccando sulla croce, poi fine lista (end list) e l'elemento viene suddiviso. Dopo cambiamo il numero di suddivisione per adattarci all'elemento più piccolo: 1, 10, 1 poi elements, clicchiamo sull'elemento ed end list.
Con mesh del tutto identica abbiamo meshato il tubo più grande la fettina di tubo più piccola. Abbiamo 481 nodi. Suddividiamo ulteriormente? No,cosi gira + veloce.
Ora abbiamo la mesh ed impostiamo i vincoli: controlliamo che non ci siano nodi apparentemente sovrapposti, ma non coincidenti, quindi facciamo mesh generation, sweep, tolleranza di default ((è già 4 ordini di grandezza inferiore al nostro elemento), se fosse 2 mm collassano tutti gli elementi cosi non collassa nessun elemento perché troppo piccolo), nodes, collassano i nodi + vicini, all exist. Toglie 8 nodi duplicati poi rifacciamo il controllo per non avere tagli nella struttura che non vediamo.
A questo punto abbiamo definito completamente la geometria, andiamo ad impostare un materiale geometric properties creiamo una nuova scheda geometrica di tipo strutturale assialsimmetrico di tipo solido che rappresenta materiale massiccio e con geometria tipo meccanico assialsimmetrico solido a nome “assialsimmetrico”, andiamo ad assocciare la scheda a tutti gli elementi che esistono, elements add exist 410 elementi associati alla tipologia della scheda.
Procedimento: geometric properties, new, structural, aximmetric, solid, poi clicchiamo su name, scriviamo assialsimmetrico, poi elements, add, all exist, end list.
Torniamo al menù principale e definiamo le proprietà del materiale. Material properties, creiamo una nuova scheda, materiale di tipo standard e lo chiamiamo alluminio (110 MPa), proprietà generali mettiamo la densità (2.7e-9 tonnellate al mm cubico), ma non verrà usata nei calcoli. Poi proprietà strutturali young moduls 70000, Poisson's Ratio 0.3, poi se vogliamo stare nel range di elasticità applichiamo la plasticità. Associamo ad alluminio tutti gli elementi che esistono, per controllare clicchiamo id materials e colora di rosa tutti gli elementi a cui è applicato il materiale.
Material properties, spunto material properties, new, name mettiamo alluminio, invio, entriamo in data categories, general, inseriamo il valore di mass density 2.7e-9, invio, ok, entriamo in structural, inseriamo il valore di Young's modulus di 70000, invio e il valore Poisson's ratio di 0.3, invio, ok, selezioniamo elements, add, all exist, end list.
Ora andiamo ad impostare le boundary condition: per prima la pressione interna, new, structural, edge load, la chiamiamo pressione_interna, proprietà, pressione, 1 MPa (non ci porta a snervamento il materiale, in questo caso anche perché non abbiamo impostato il carico di snervamento) e invio, edge add, selezioniamo cliccando tutti gli edge del bordo interno e poi diamo fine lista.
Boundary conditions, new, structural, edge load, poi entriamo in properties, spuntiamo pressure, mettiamo 1 MPa, invio, ok, selezioniamo con il mouse i nodi, end list.
Gli diamo una pressione e lui si calcola i carichi nodali che sono funzione del raggio.
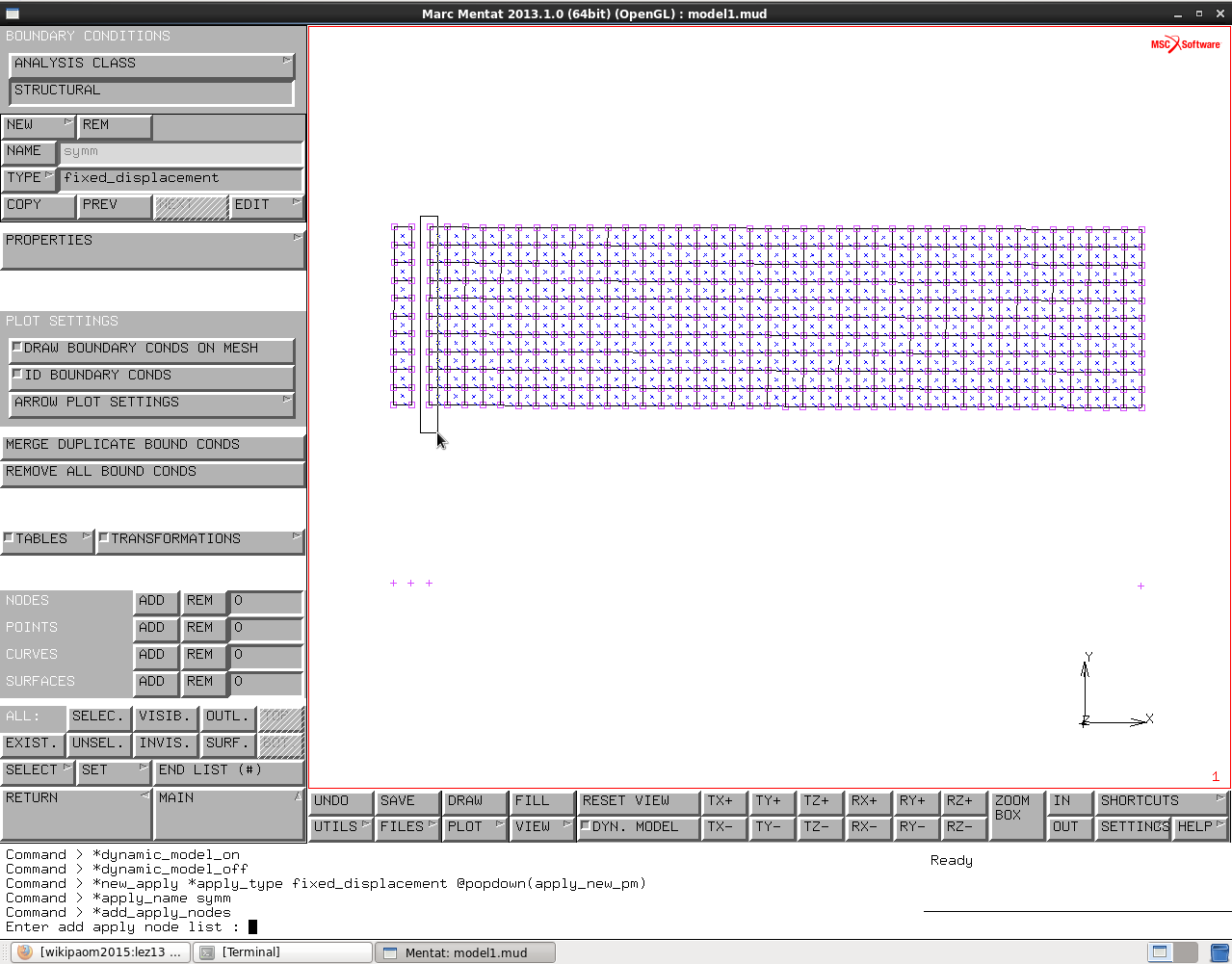
Vincoli: mettiamo un vincolo di posizionamento che consiste nel bloccare 1 gdl per ogni fetta (grande e piccola) in spostamento assiale. Possiamo mettere anche un vincolo di simmetria cosi diventa lungo 80 mm, senza elementi in più.
Creiamo un vincolo new, strutturale, di tipo fixed displacement, che può essere un vincolo di simmetria o di posizionamento. Lo chiamiamo vincolo di simmetria. può essere di due nature perché bloccando lo spostamento x a valore nullo posso ottenere entrambi gli effetti. Decidiamo di usarlo come vincolo di simmetria e come effetto collaterale otteniamo il condizionamento assiale e lo applichiamo ai nodi verticali esterni a sinistra della seconda figura che diventano appartenenti ad un piano di simmetria. Applichiamo lo stesso vincolo anche al nodo inferiore a sinistra della prima figura. Per questa struttura è vincolo di simmetria, per l'altra di posizionamento. Lo chiamiamo invece di “simmetria”, “simmetriaeposizionamento” così ci ricordiamo di entrambi. Boundary conditions, new, structural, fixed displacement, poi andiamo in properties, attiviamo displacement x, con valore 0, selezioniamo con mouse i nodes, end list.
Ora il problema è pronto per essere lanciato.
Menu principale, jobs, new, structural, properties: initial load, pressione interna, simmetria e simmetriaeposizionamento attivati.
JOBS.PROPERTIES.JOB RESULTS. e quindi selezioniamo stress, total strain, elastic strain, plastic strain (=0), equivalent von mises stress, ok, poi “ANALYSIS DIMENSION” –> axialsimmetric invece che 3D. Lanciamo il calcolo elastico, ora Jobs, elements types, analisys class- structural, analisys dimension - axymmetric, solid, per i quadrilateri a 4 nodi in full integration ho 10, ok, all exist. Tutti gli elementi della struttura sono di tipo 10.
Qual è la discretizzazione? Campioniamo lo stato tensionale in 4 punti di gauss, un elemento con 4 punti di gauu può essere 25 - 50-75- 100% plasticizzato. Se abbiamo elemento ad 1 solo punto di plasticizzazione è più semplice. È meglio non usare molti punti di plasticizzazione, non è realistico. Non usare elementi parzialmente plasticizzati.
Ora facciamo run, submit, apriamo il file dei risultati.
Per andare ad analizzare i risultati:
POSTPROCESSING RESULTS -> OPEN POST FILE scelgo come SCALAR PLOT :CONTOUR BANDS
Vado quindi ad analizzare i diversi tipi di SCALAR: Comp 33 of stress
NOTA BENE: Comp 11 of stress: indica una tensione assiale i ìn direzione x. Comp 22 of stress: indica una tensione radiale Comp 33 of stress: indica una tensione circonferenziale

Notiamo che, essendo stato applicato 1Mpa di pressione al bordo interno, si ottiene 1.749 MPa di tensione circonferenziale al bordo interno. Per controllare se questa tensione che risulta sia corretta si apre un foglio Maxima e si confronta il valore ottenuto (1.749) con quello calcolato in Maxima (1.66666); quindi il valore ottenuto con Marc Mentat è leggermente eccessivo ma rientra nell’ordine di errore. Si noti di come la singola fetta di tubo è rappresentativa dell’oggetto complesso e le curve di livello sono esattamente le stesse; questo è dovuto al fatto che questa fetta è libera di contrarsi assialmente perchè si è solo messo un vincolo di posizionamento ma tutto il resto dei due bordi sono liberi di muoversi; questa fetta è quindi in uno stato di tensione piana (la tensione in z dovrebbe essere nulla). In questo caso nessuno vieta alla $\sigma_z$ di essere nulla , mentre nel modello della lezione precedente questa era un’ ipotesi di partenza e quindi non era verificabile, in questo caso nessuno vieta alla $\sigma_z$ di essere nulla perchè, per come è costituita la struttura, c’è possibilità di avere una tensione assiale arbitraria.
Comp 11 of stress
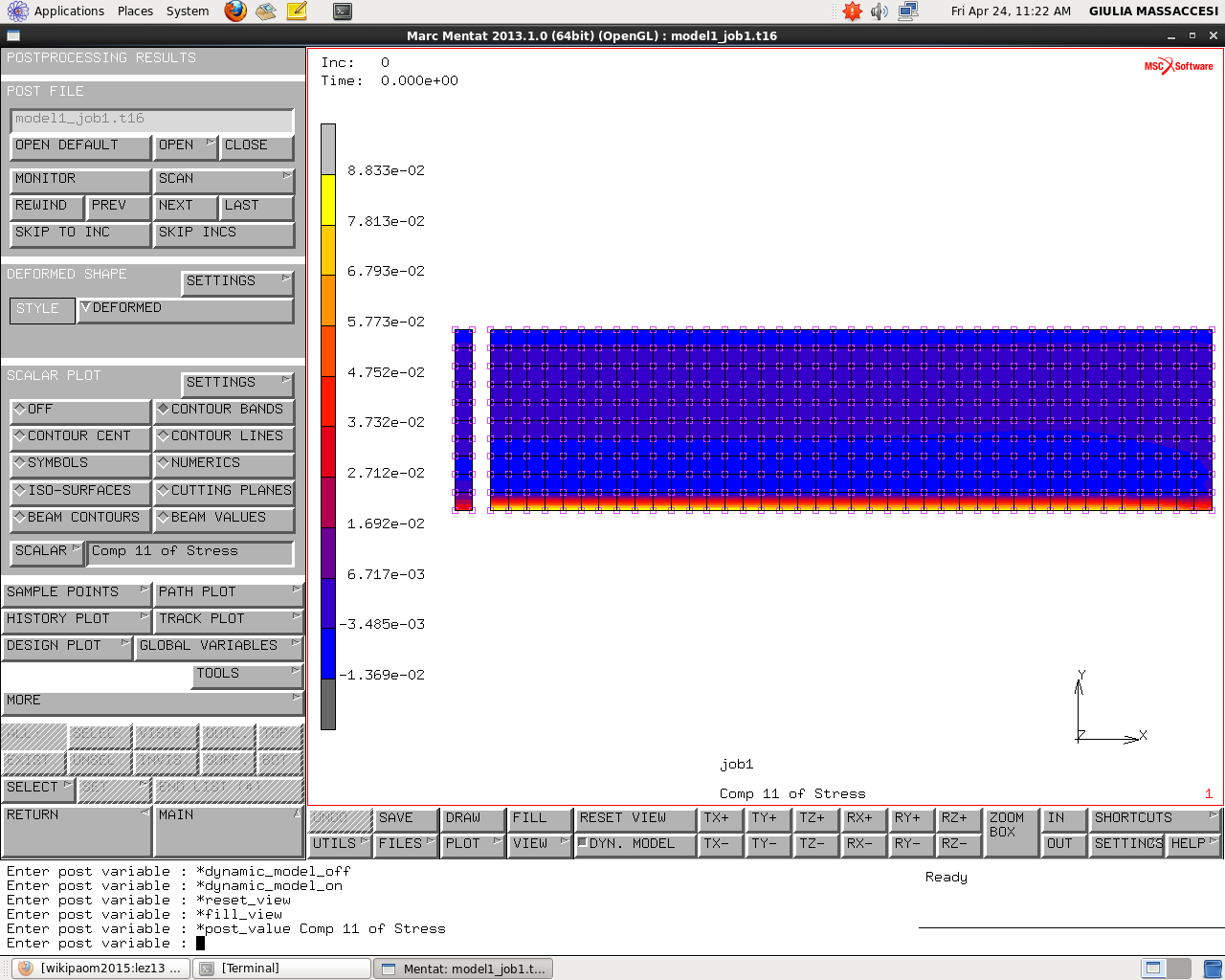
Per verificare se l’ ipotesi di stato di tensione piana sia applicabile al tubo vado a vedere la Comp 11 of stress che non è nulla in senso assoluto ma è comunque dell’ordine di $10^(-1)$ ovvero al di sotto di uno o due ordini di grandezza rispetto la tensione circonferenziale; quindi non è nulla ma è piccola (infittendo la mesh dovrebbe calare ulteriormente). Quando non impongo delle ipotesi di partenza di stato di tensione piana (come la lezione precedente) ma la vado a verificare, non è verificata in maniera esatta e precisa ma possiede un ordine di grandezza al di sotto di 1 o 2 ordini di grandezza delle altre componenti tensionali.

Si noti che c’è una piccola deviazione nell’intorno dell’area finale, che è dovuta da un errore numerico e che in teoria dovrebbe calare al calare della mesh.
Comp 11 of Total Strain e Comp 11 of Plastic Strain
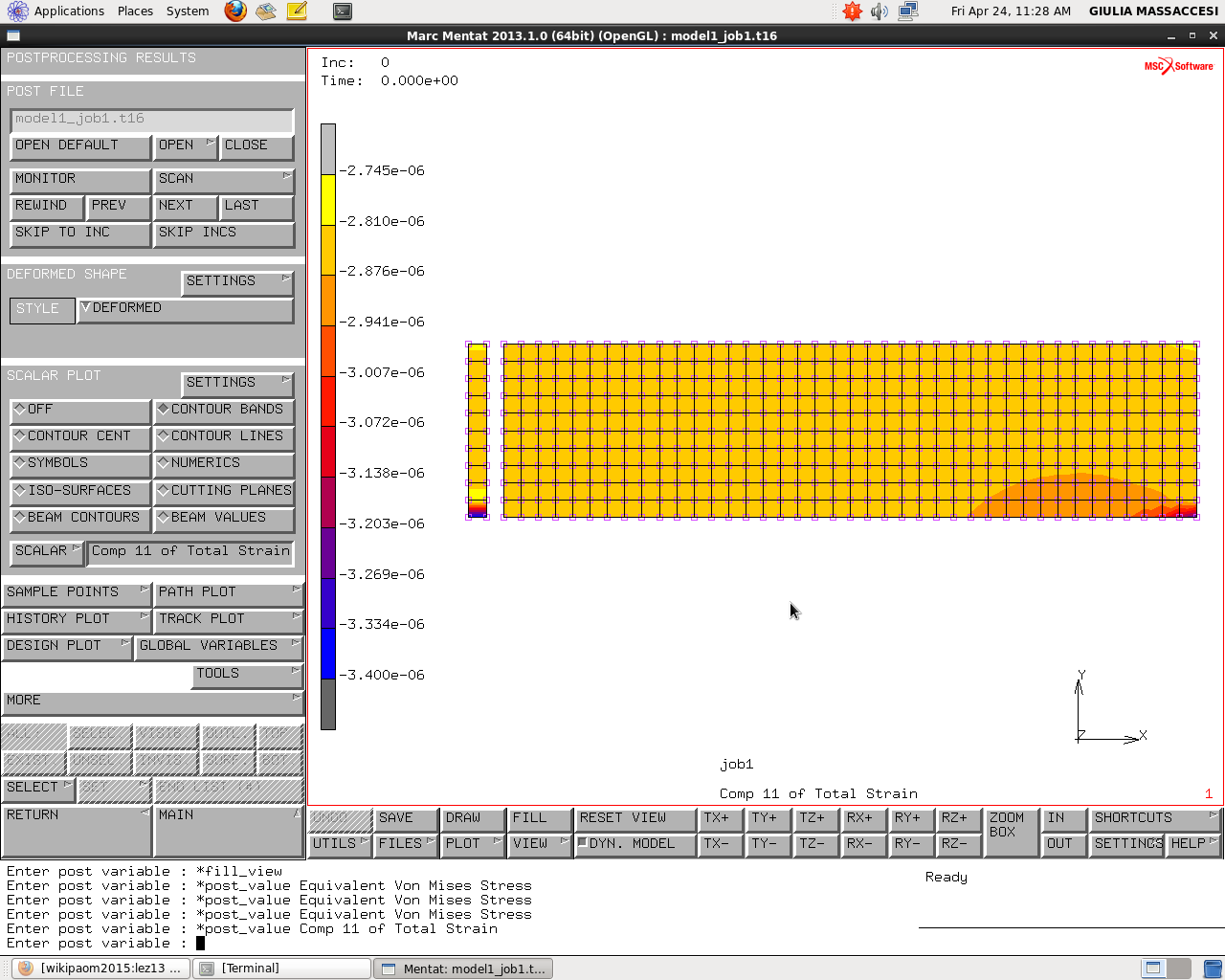
Si controlla ora se effettivamente se la struttura deforma uniformemente lungo l’asse ovvero se tutte le fette si compattano in maniera uniforme. Ciò lo si va a vedere andando a guardare la Comp 11 of Total strain (la deformazione lungo x, in direzione assiale) e si nota che è compresa tra una forchetta che va da $3.4e^(-6)$ a $2.7e^(-6)$ mentre nel tubo finale è molto più informe. Nella teoria della tensione piana questa quantità, ovvero la deformazione z, dovrebbe essere una quantità libera cioè se impongo una tensione in direzione assiale nulla lascio libera questa tensione. In realtà per una particolare proprietà del tubo pur imponendo nulla la tensione in direzione fuori piano la deformazione rimane costante lungo la struttura. Qui nel tubo appare costante con uno sporco che cala al calare delle dimensioni dell’elemento.
QUINDI quello che si sta vedendo è la componente x dello strain (allungamento lungo la direzione x) e si nota di come sia puramente dovuta alla quota elastica e non dalla elastica e plastica; infatti se si va a controllare la deformazione plastica (Comp 11 of Plastic strain) questa è omogeneamente nulla.
Equivalent Von Mises strain

L’ Equivalent Von Mises strain è omogenea e dà valori di 2.33 che indicano un piccolissimo snervamento. Displacement x
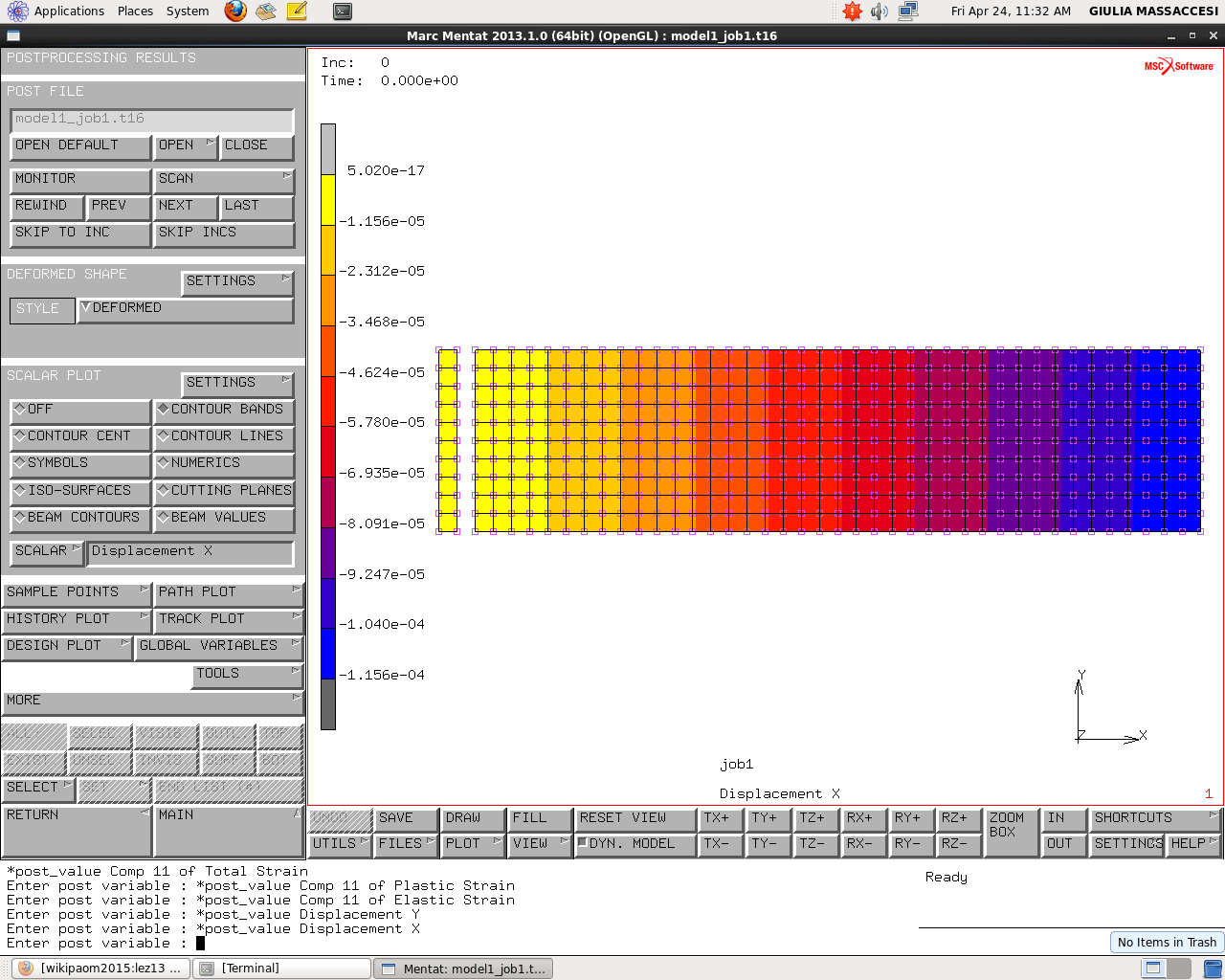
Notiamo come gli spostamenti in direzione x sono omogenei (con un piccolo sporco finale) lungo la sezione, ciò indica che tutti i punti di questa sezione si muovono in direzione assiale insieme.
OSSERVAZIONI
La particolarità del tubo analizzato è che quest’ultimo è una struttura spessa che possiamo però modellare in tensione piana ; in questo caso non si è imposta una deformazione omogenea lungo la fettta ma, viceversa, una tensione assiale nulla ottenendo come risultato una deformazione omogenea in elasticità esatta. Nel metodo ad elementi finiti queste ipotesi valgono con i limiti della discretizzazione. Quindi il metodo di modellazione in tensione piana del tubo elastico è sostanzialmente valido e legato all’entità dell’errore.
Modellazione plastica
Proviamo a vedere cosa succede se usiamo una modellazione plastica: Vado a modificare il modello quanto, per applicare una modellazione plastica, basta impostare un modello non lineare elastoplastico.
Per andare in stato plastico, vado a prendere dal libro di Progettazione assistita di organi meccanici (del Prof. Strozzi) ricavo pressione da applicare al bordo interno di tubo in funzione di quanto è la porzione di tubo che voglio plasticizzare. Se applico 68.66Mpa come pressione interna al mio bordo non lineare, al bordo interno questo tubo verrà snervato fino a metà sezione ed avrà un raggio di transizione tra zona plastica e elastica dell’ordine di 15. Nel tubo quindi ci sarà una zona plastica dal bordo interno fino ad un certo raggio di tranziozione e poi una zona elastica residua dal raggio di transizione al bordo esterno. Questa formula calcola la pressione da un voluto raggio di transizione e non verrà esattamente uguale nel FEM un po per l’errore di discretizzazione ma anche perchè è vìcalcolato con tresca o $tao$ max mentre il marc usa la Von Mises. Dobbiamo cambiare il nostro modello:
MAIN->BOUNDARY CONDITION -> pressione interna->proprietà e si cambiano le proprietà della p da 1 Mpa a 68.66 (dovrebbe dare snervamento fino a metà sezione).
Se lancio un’analisi adesso :
JOB-> RUN->SUBMIT
La tensione secondo Von Mises risulta 153.3 Mpa nel bordo interno quindi ho una tensione secondo Von Mises che eccede il limite di elasticità.
Si può anche vedere quanto è l’area al di sopra della plasticità ,ovvero l’area che sfonda il muro dei 110, utilizzando una visualizzazione grafica:
OPEN POST FILE ed apriamo il file dei ridultati con la pressione maggiorata metto la SCALAR: Equivalent Von Mises Stress
e guardiamo la mappa della Von Mises e vediamo che nel suo punto più elevato supera i 110MPa (che abbiamo supposto essere lo snervamento del materiale.
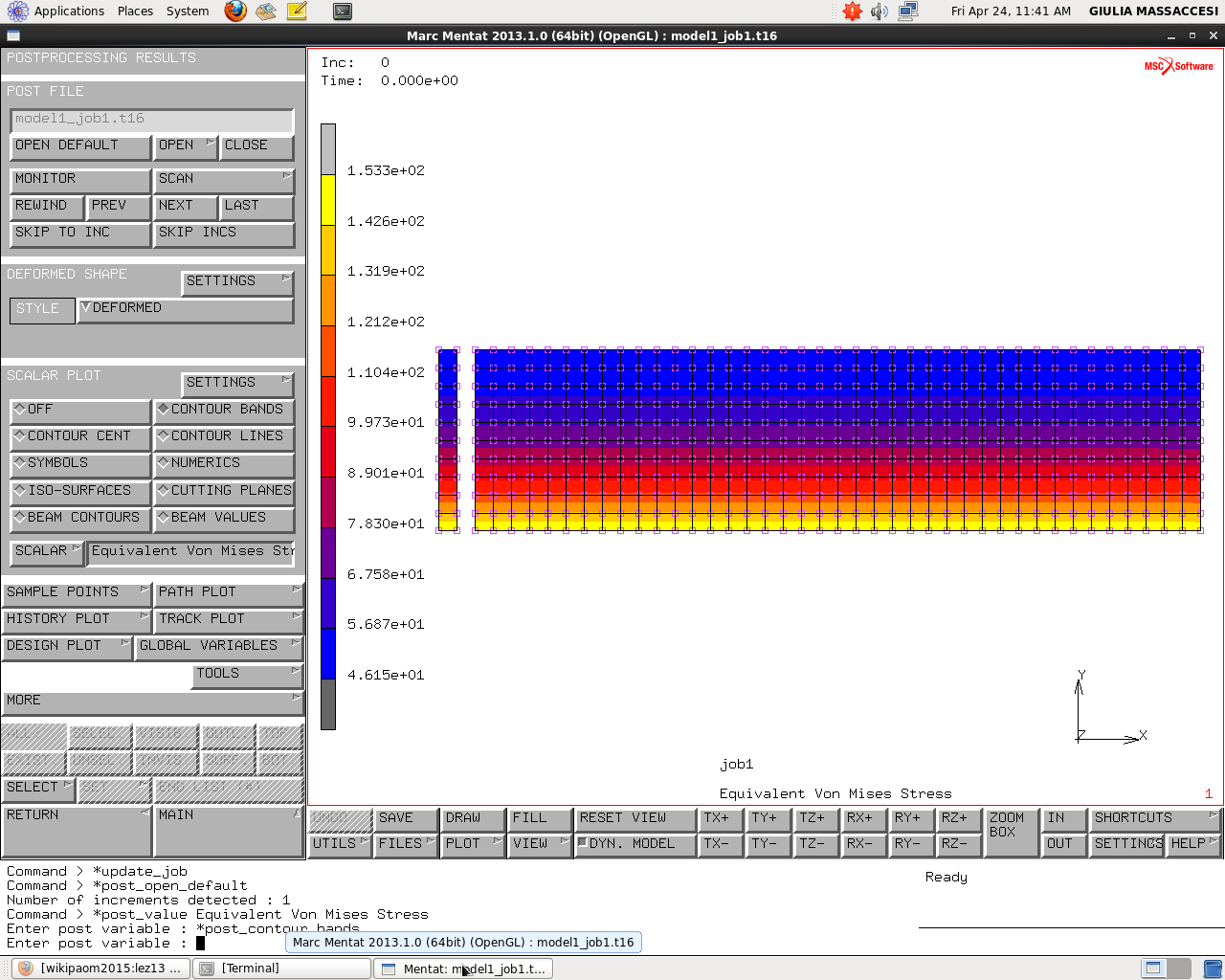
SCALARPOLOT->SETTINGS->MANUAL (da 0 a 110)
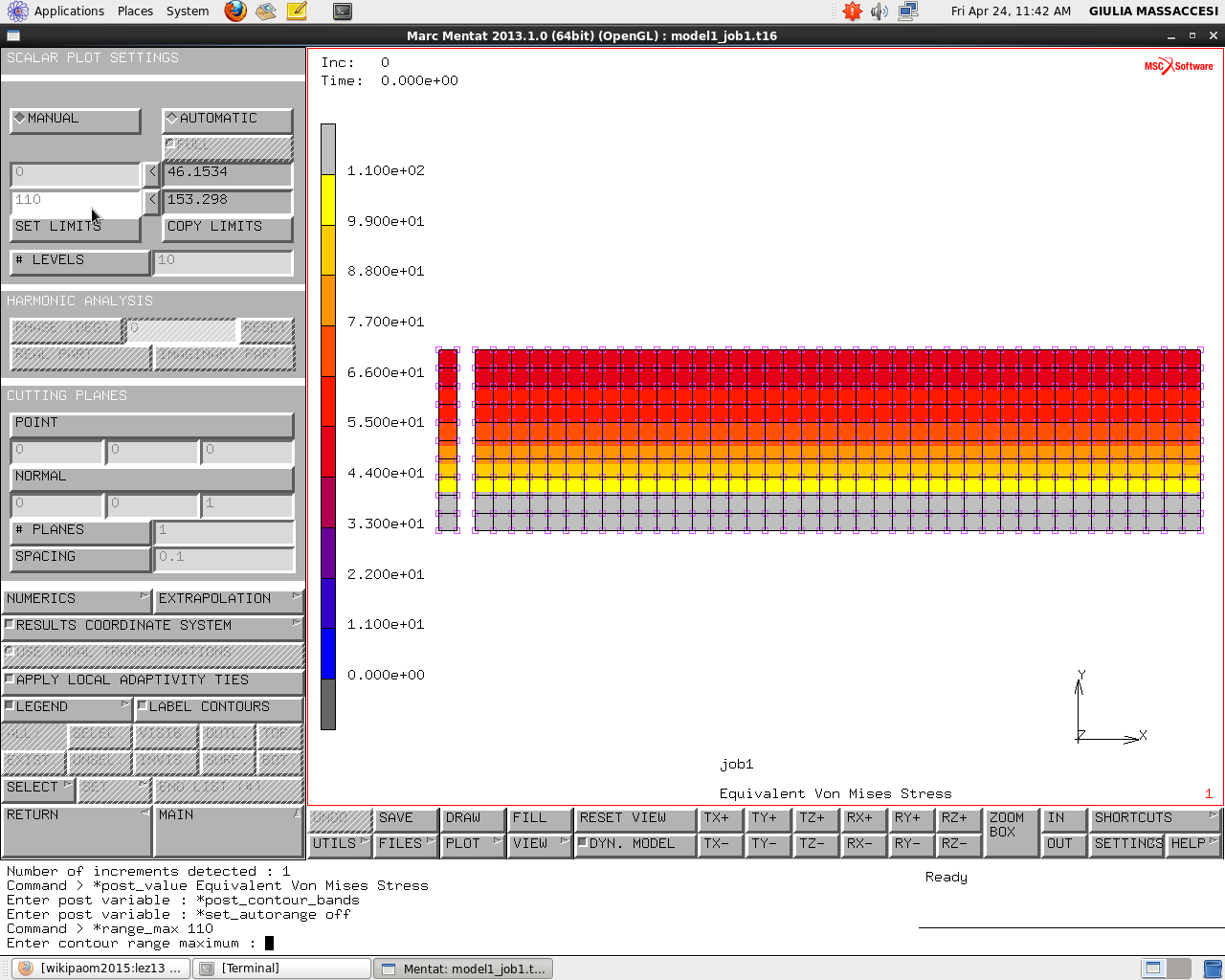
Applicando una scala manuale che va da 0 a 110, possiamo isolare un fuori scala notando che tutti gli elementi che sono oltre i 110MPa in Equivalent Von Mises Stress sono evidenziati di grigio. Nel nostro caso si nota che due file di elementi superano lo snervamento.
Per sapere qual’è il valore su cui è stato effettuato lo sweech elastico plastico da parte del solutore (ovvero sui punti di integrazione) vado nel menu:
EXTRAPOLATION-> attivo il TRANSLATE (traslazione ai nodi) e disattivo il NODAL AVERAGING (la media nodale) cliccando su OFF
Con il comando Translate prendo i quattro valori e li considero direttamente come valori nodali, quindi le mappe colorate son costituite coi valori dei punti di integrazione. Togliendo la media nodale vedo esattamente i punti di integrazione dell’elemento. Quindi se dovessi stimare un’area interessata dal fenomeno di plasticizzazione da questo calcolo lineare potrei dire che la plasticizzazione avviene solo sui due primi strati dell’ elemento in cui ho punti di integrazione che superano il valore dello snervamento, ovvero la plasticizzazione interessa le prime due file di elementi ossia un raggio che va fino ai 12mm non tenendo conto alla distribuzione dei carichi dello stato tensionale associata alla plasticizzazione (questo approccio vale solo se le aree plasticizzate sono molto piccole).
Chiudo il file dei risultati ed imposto un vero e proprio calcolo non lineare. Prima di tutto salvo con nome:
SAVE AS-> TUBO_ELASTICO in seguito salvo nuovamente col nome: SAVE AS-> TUBO_ELASTOPLASTICO
TUBO ELASTOPLASTICO
Attiviamo la plasticità della struttura così il sistema diventa elastoplastico e quindi disssipativo:
MAIN MENU->MATERIAL PROPRIERTIES -> STRUCTURAL PROPERTIES -> attivo PLASTICITY ->impongo uno YIELD CRITERION: VON MISES ->porto a 110 YELD STRESS->OK
Così facendo applico uno snervamento di 110Mpa, mettendo solo uno snervamento ottengo solo un elastoplastico. Se ci fosse incrudimento questo sarebbe isotropo e non cinematico (VEDI Appendice 1). Adesso il modello è diventato non lineare, quindi il fenomeno è diventato non dissipativo e quindi lo stato della struttura è funzione della storia di carico.
Bisogna definire quindi una storia di carico:
MAIN MENU->BOUNDARY CONDITIONS->TABLES
una table è in generale una funzione che ci permette di definire la storia del tempo; questa funzione è funzione del tempo e va a modulare il valore di 68.66 Mpa. La funzione va tipicamente da 0 ad 1. Per creare questa funzione modulante lo si fa andando dal menu TABLES creiamo una nuova tabella: (si hanno fino a 4 variabili indipendenti) la funzione la chiamiamo “modula pressione”, impostiamo il tipo della variabile e mettiamo “time”
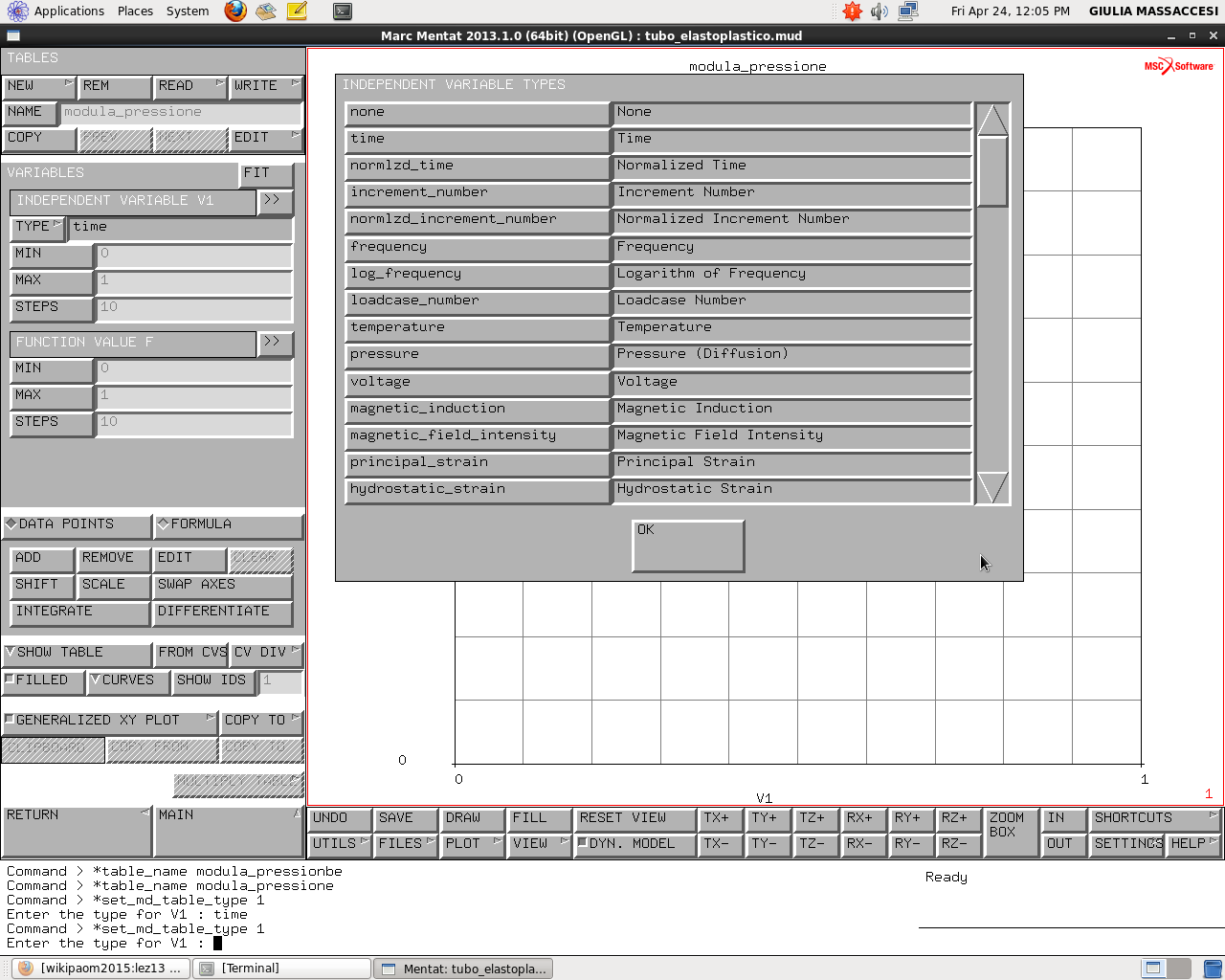
Definiamo una storia di: carico scarico e ricarico ;ovvero definiamo una legge nella variazione del tempo della mia pressione inserendo 4 punti, in particolare quelli in cui la funzione modulante f(t): -quando t = 0 la modulante vale 0; -quando t=1 la modulante vale 1 (la modulante cresce fino a raggiungere un valore unitario al tempo 1); -quando t=2 la modulante vale 0; -quando t=12 la modulante vale 10; Questa funzione si può esplicitare per “formula” o “data points”, noi scegliamo data points ed andiamo ad aggiungere punti:
clicco DATA POINTS->ADD, inserendo: (0,0) (1,1) (2,0) (12,10)
NOTA BENE (1): per scalare il grafico e fargli contenere tutti i punti FILL NOTA BENE(2): l’ordine con cui si danno i punti non è importante.

Dal grafico ottenuto notiamoche abbiamo fatto un caricamento, scaricamento e poi ricaricamento fino a che il tubo esplode.
Dopo aver fatto la tabella:
BOUNDARY CONDITION->PROPERTIES->TABLE aggiungo la tabella “modula_pressione” ->OK

Per passare dalla visualizzazione della tabella a quella del modello :
SHORTCUTS-> MODEL (da table)
E mi torna a mostrare il modello.

Per adesso abbiamo definito la curva di carico, scarico ed esplosione ma non abbiamo definito il tempo della nostra analisi, in particolare le storie di carico si vanno a definire nel menu LOADCASES (storia di carico) e definiamo 3 pezzi di storia di carico: -carico -scarico -continua a caricare
Lodcase di carico
LODCASES->NEW->NAME:carico->TYPE:static
Le proprietà del pezzo di storia del carico dicono quali carichi e quali vincoli sono attivi in questo troncone di storia di carico, come si può vedere cliccando:
PROPERTIES->LOADS-> vediamo che sono selezionate la symm e la pressione_interna TOTAL LODCASE TIME->1
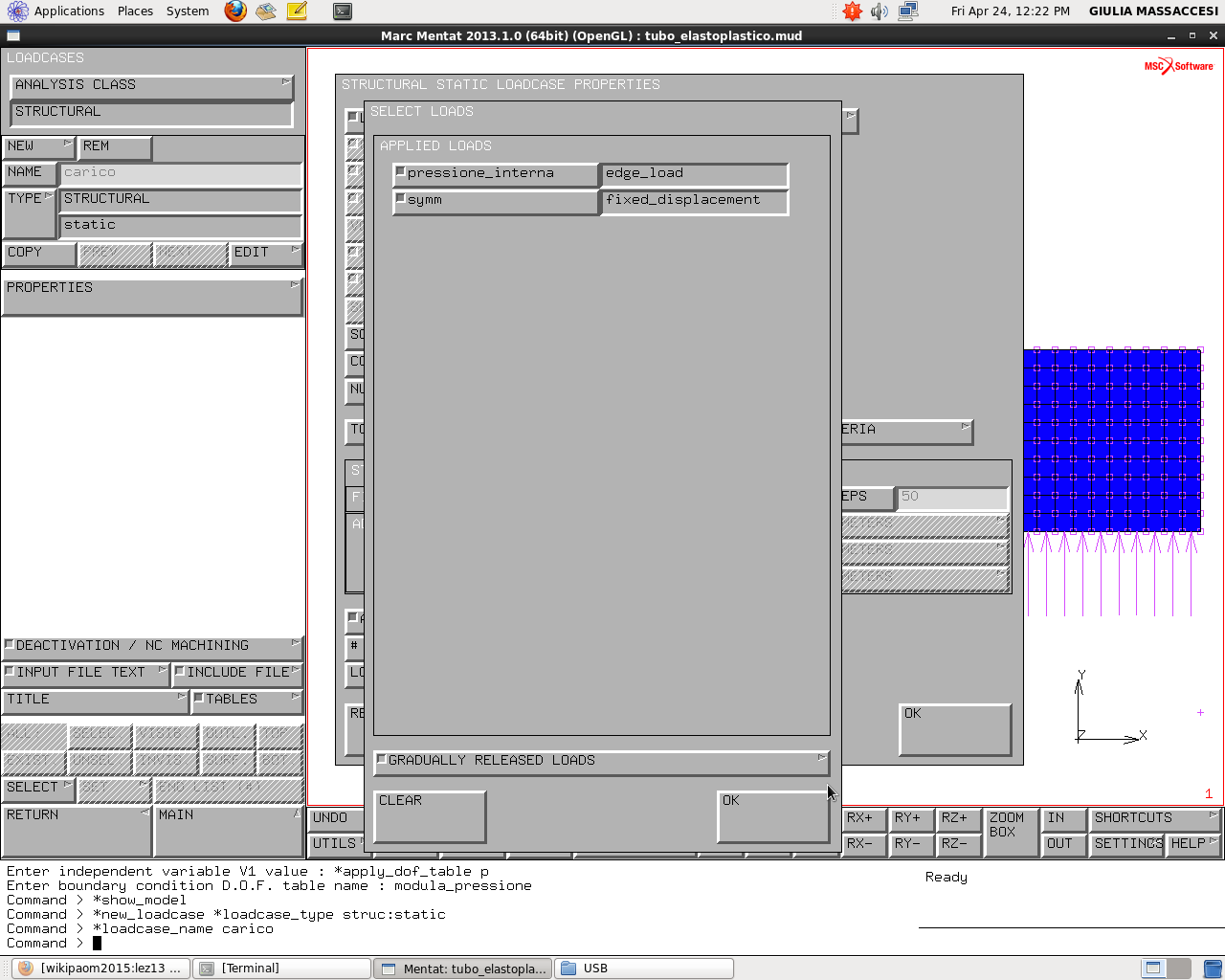
Il TOTAL LODCASE TIME indica quanto dura questo troncone di carico, nel nostro caso dura un secondo (46)
In seguito verranno analizzati i singoli comandi nella sezione STRUCTURAL STATIC LODCASE PROPERTIES e verranno fatte alcune piccole modifiche:
SOLUTION CONTROL

Sono i parametri di Newton Rapson (NR), il NR è un procedimento iterativo in questo caso si vede nel numero massimo di iterazione che è 10 ed il minimo che è 0. NOTA BENE con il termine RECICLE Marc intende “iterazioni di Newton Rapson”
-FULL NEWTON-RAPSON: quello che utilizzeremo -MODIFIED NEWTON-RAPSON: in cui non ricalcolo lo Jacobiano ogni volta ma utilizzo lo Jacobiano vecchio , non lo useremo -N-R WITH STRAIN CORRECTION: non lo useremo -NON POSITIVE DEFINITE: se attivato dichiariamo che la matrice è singolare, attiva anche una procedura automatica -PROCEED WHEN NOT CONVERGED: Se dopo 10 iterazioni non è andato ad andare avanti continua fino a che non arriva a convergenza: -ASSEMBLY EACH ITERATION: non lo useremo
Inseriamo: MAX # RECYCLES -> 10 MIN # RECYCLES -> 0
CONVERGENCE TESTING:

Indica la convergenza di newton rapson quando i residui sono in norma più piccoli in una certa soglia: -RELATIVE:
- RESIDUALS: vuol dire che dichiaro la convergenza quando ill max residuo è il 10% della massima reazione vincolare (perchè è una convergenza relativa)
- DISPLACEMENTS: dichiaro la convergenza quando l’ultima correzione degli spostamenti è in modulo il 10% dello spostamento totale, anche se il 10% è un po tanto ALLORA NOI METTIAMO 0.001
- RESIDUAL AND DISPLACEMENT:per cui la convergenza viene dichiarata se sussistono ambedue le condizioni di convergenza raggiunta ai regimi ed agli spostamenti
-ABSOLUTE:
- RESIDUALS: il massimo valore assoluto in Newton che può avere residuo
RELATIVE->RESIDUALS AND DISPLACEMENT->RELATIVE DISPLACEMENT TOLERANCE:0.001
STEPPING PROCEDURE
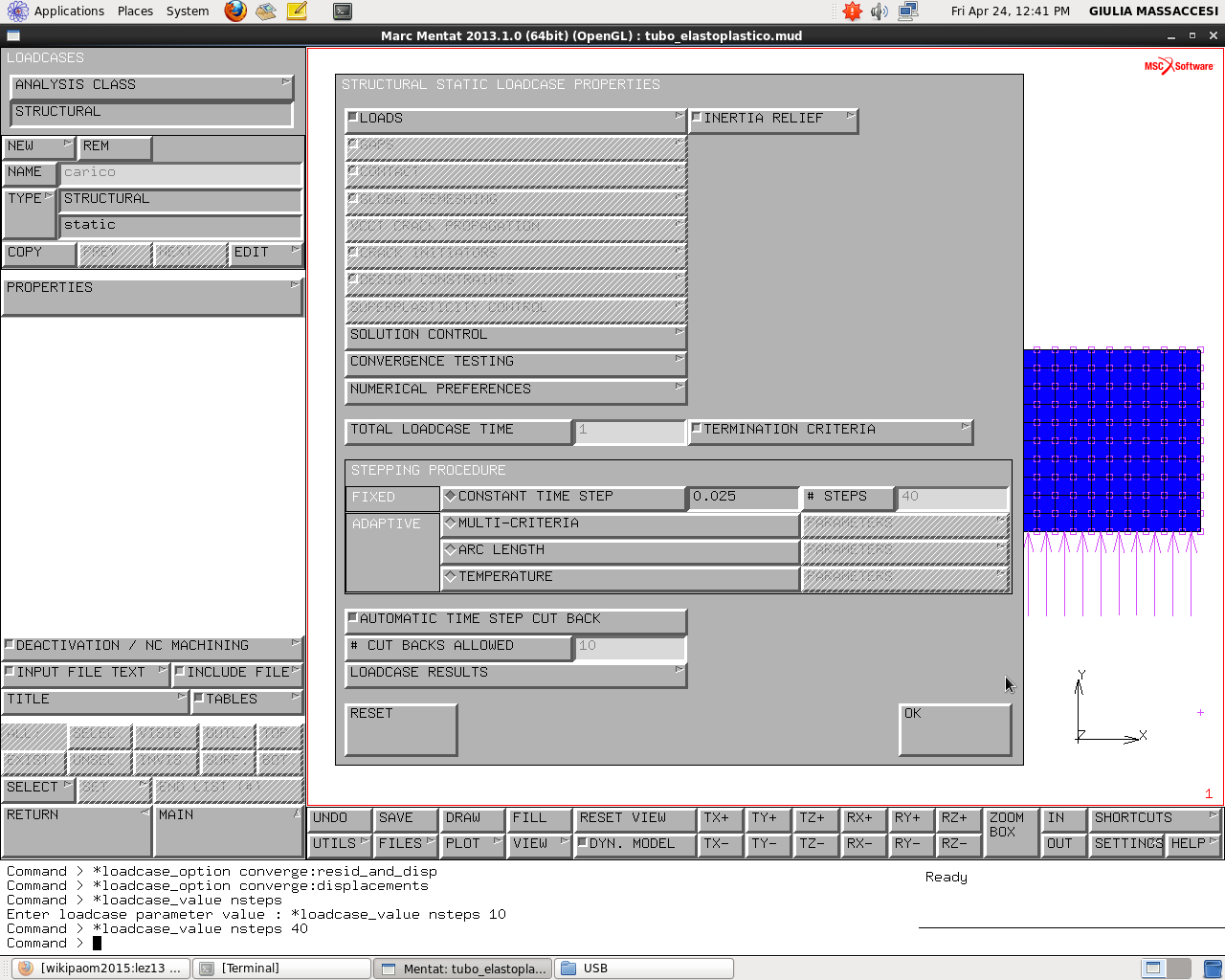
CONSTANT TIME STEP
-#STEPS
Quando si ha un sistema di carico non lineare e la storia di carco va percorsa a piccoli passettini se metto 10 passettini vuol dire che la storia di carico viene divisa in 10 passi del 10%, se invece metto 40 vuol dire che applico un passo ogni 1/40 della storia di carico. Ogni passo lancio un Newton Rapson ovvero da un istante i ad un istante i+1 comorta un’iterazione di newton rapson. Questi istanti temporali sono chiamati incrementi, ogni passaggio da incremento i ad incremento i+1 comporta un certo numero di ricicli che sono le iterazioni del newton rapson. Più sono gli istanti temporali e più i salti son piccoli e più la soluzione dell’incremento precedente è vicina alla soluzione dell’incremento successivo e quindi meno fatica fa Newton Rapson a convergere; viceversa se divido in 10000 incrementi, ho almeno 10000×2 ricicli di Newton Rapson (2 per ogni incremento) il che vuol dire che devo risolvere il sistema lineare associato a quella struttura 20000 volte; per questo noi usiamo pochi nodi, perchè ci danno un oggetto computazionalmente snello. Bisogna fare attenzione perchè ogni riciclo di un calcolo non lineare costa come un calcolo lineare, quindi non devo mettere nè troppi nè pochi incrementi. Nel problema dissipativo avere un passo fine sugli icrementi temporali vuol dire definire in modo preciso la storia di carico, essendo la soluzione in funzione della storia di carico, avere un’alta risoluzione nella risoluzione della storia di carico vuol dire avere una soluzione precisa.
NOTA BENE se si ha un dubbio si lancia a 40 steps e poi si lancia ad 80, se non cambia niente allora 40 va bene
Se Newton Rapson non converge dopo 10 tentativi riprovo Newton Rapson su un salto che è la metà (attraverso un cut back), l’intervallo di calcolo può essere 2^10 volte più piccolo dell’intervallo iniziale, se non converge esco con l’errore .
immagine niko confrontata
-CONSTANT TIME STEP Indica il tempo che si impone per percorrere un passettino
ARC LENGHT Non ho step temporali imposti ma procedo per spostamenti costanti, ovvero ogni step voglio andare avanti per 1 mm e non mi interessa quanto ci vuole per fare 1mm, si usa per problemi istabili che non affrontiamo nel nostro corso.
Imponiamo: # STEPS->10
LODCASE DI SCARICO E RICARICO FINO A ESPLOSIONE (PRESSURIZZAZIONE)
copio due volte (ciccando copy) il lodcase di carico. Il carico e scarico sono due lodcases gemelli, l’unica cosa che modifico è nel terzo impongo # STEPS: 40
In seguito:
MAIN MENU-> JOBS->PROPERTIES ->SELECT INITIAL LOADS->disattivo la pressione interna->OK
D isattivando la pressione interna sottolineo il fatto che all’istante 0 non applico carico e parto da scarico.

Clicco su AVAILABLE->seleziono in ordine:carico,scarico e sicarico_fino_a_esplosione->OK

Selezionando la sequenza dei lodcases che voglio applicare nel mio job (carico, scarico e ricarico fino a esplosione) carico nell’istante 0, scarco, processo la storia di carico “carico”, processo la storia di carico “scarico” ed infine processo il lodcase “ricarico fino a esplosione”.
Infine clicco:
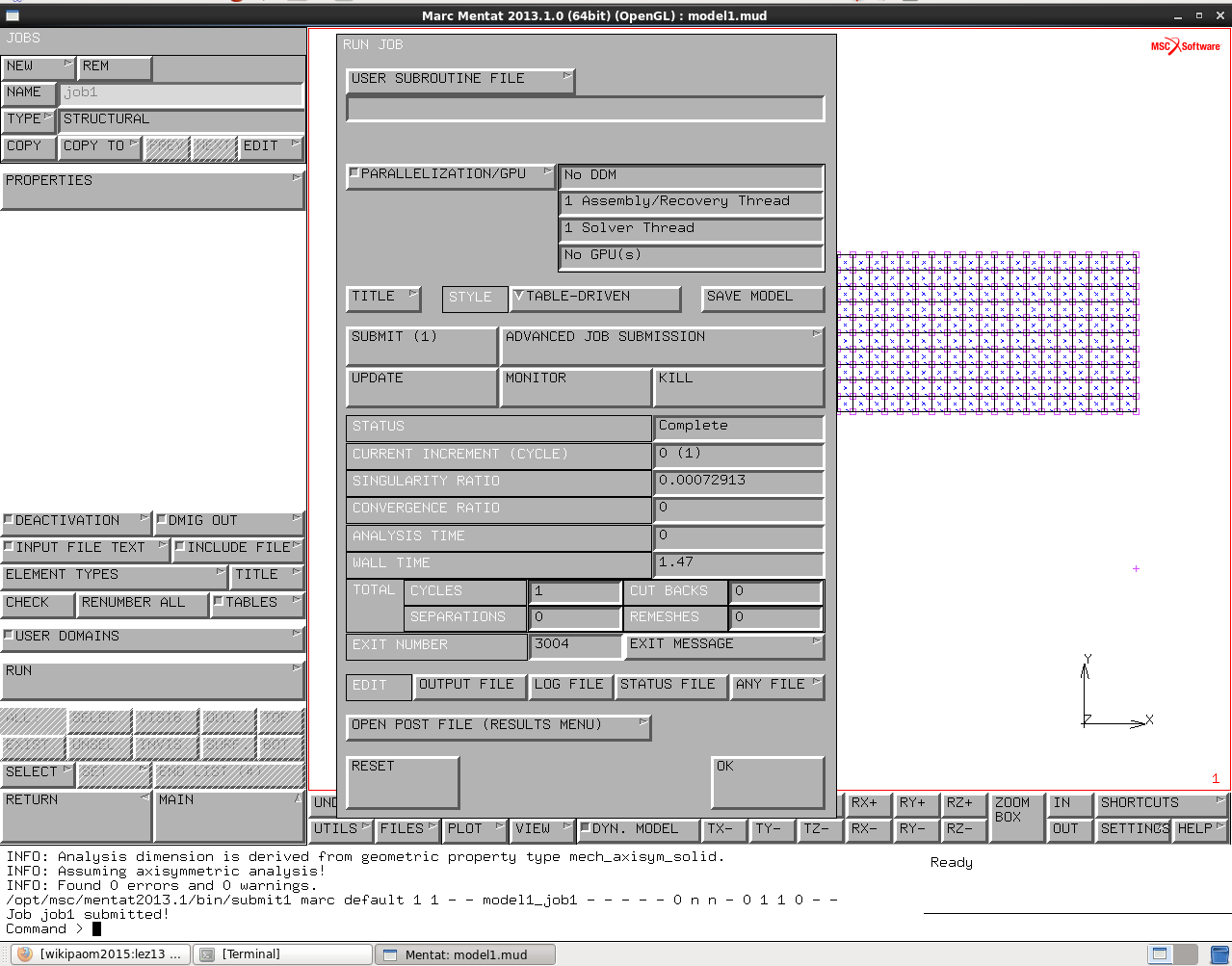
RUN->JOB

Aspetto qualche secondo (Fino a che lo status non è “Complete”, come in figura) ed osservo le varie indicazioni: CURRENT INCREMENT: Indica il numero di ricicli effettuati, ogni volta che I ricicli non vanno a convergenza inseriscono un cutback.
ANALYSIS TIME:3.37 è il tempo su questa scala associate allo step 135, si può andare a vedere qual’e l’unità del tempo al quale si è impiantato il calcolo.
EXIT NUMBER: non è 3004 ma è 3009, la taglia del time step è diventata troppo piccola. Tutti i risultati fino all’incremento 135 escluso sono stati scritti sul nostro t16.
Analizzando i vari risultati attraverso:
OPEN POST FILE
Eequivalent Von Mises Strain
Per vedere l’area effettivamente snervata, lo faccio sogliando al di sotto dello snervamento, tutto quello sotto soglia che è compreso tra 109.9 e 110,.
PLOT->SETTINGS e soglio a 109.9

vediamo che 3 file di elementi sono effettivamente snervate (dal calcolo lineare ne avevamo 2 di file snervate) , la teoria mi dice che lo snervamento deve avvenire a metà del tubo.
Displacement x
DEFORMATION SCALING-> AUTOMATIC SPOSTAMENTI ASSIALI (displacement x)

Noto che in effetti l’espansione non è lineare, ho una parte plastica che tende a spanciare (incremento temporale di 76). La fetta non mantiene espansioni costanti come il caso elastico, quindi nel caso elastoplastico non è più valida l’ipotesi che il tubo può essere modellato in tensione piana ma va modellato tenendo conto di una dilatazione differenziale in direzione assiale. nell’asse y non è nulla ma ho uno spostamento radiale
Component 11 of Stress(incremento 76)
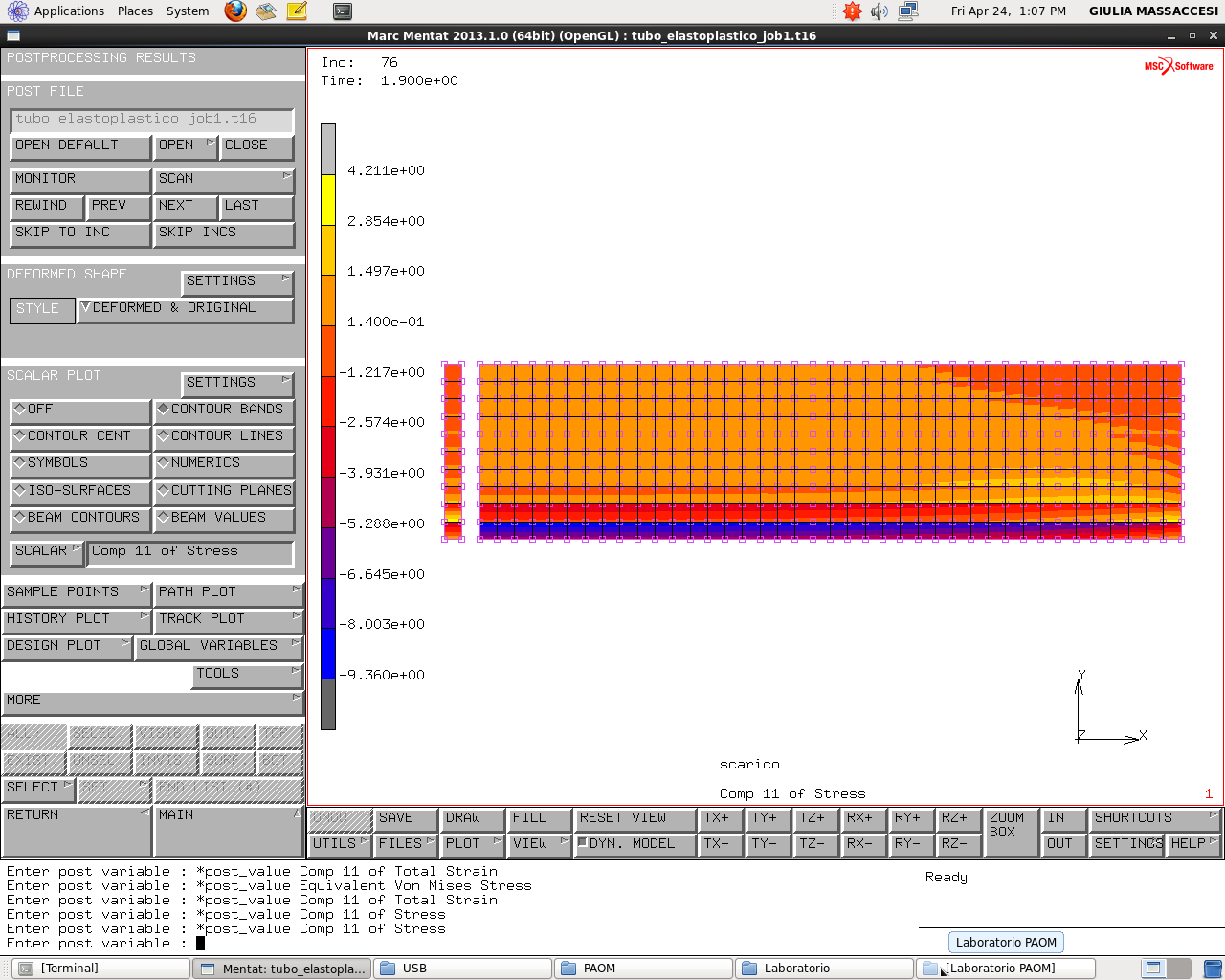
le componenti assiali di sforzo non sono nulle come nel tubo elastico.
Von Mises

all’incremento 134, il fronte plastico aumenta fino a che (in assenza di incrudimento) il materiale è interamente plasticizzato non ho più rigidezza residua.
NOTA BENE marc non lavora mai elastoplastico, ma dà sempre una piccola pensdenza di incrudimento numerico, altrimenti un elemento elastoplacizziato allora avrebbe rigidezza nulla allora punto singolare.
Appendice 1
Caricamenti non assialsimmetrici
Esistono infinite variazioni di questo elemento, per esempio si può assumere un caricamento assial simmetrico più torsione, a cui sono associato due gdl, sul piano, spostamento assiale e spostamento radiale, nonché una torsione fuori piano. Nelle varianti possibili, si può deviare dall'assial simmetria del caricamento e, dunque della deformata. Un elemento tipo è rappresentato dall'elemento 95 di Marc, assialsimmetrico, più flessione. Si considerano 5 gdl per ogni nodo, di elemento piano. - u spostamento radiale - w spostamento assiale inoltre - u', w', spostamenti, di un nodo fantasma posizionato a 180° dal nodo di riferimento - v spostamento tangenziale valutato a 90° dal punto di valutazione dello spostamento radiale, necessario per definire spostamenti di tipo tagliante associati alla flessione. Gli spostamenti di punti intermedi, sono scalati con legge cosinusoidale più costante, del tipo A+cosθ (che proiettato sul piano diviene una retta) sulla congiungente degli spostamenti assiali w, w', ciò consente di rappresentare i contributi flessionali, come in figura.
Dunque elementi piani, in funzione della costruzione, potranno avere un numero di gradi di libertà superiore a due, per ottemperare agli scopi specifici.
In questo elemento in particolare gli spostametni sono definiti da una quota costante più un contributo sinusoidale (nell'angolo θ , di rivoluzione) , ciò discende dalla teoria dell'elasticità, che afferma che per una struttura assialsimemtrica caricata circonferenzialmente in maniera costante, si abbia una risposta circonferenzialmente costante, analogamente per un caricamento in senθ o cosθ.
Per esempio per una pressione P(X;Y;θ)=f(X;Y)cos(nθ), (con n=3 si avrà la forma trilobata in figura 7), non assialsimmetrico, ma modulato su una specifica armonica, si avrà una risposta di spostamenti sulla medesima armonica, del tipo u(X;Y;θ)=g(X;Y)cos(nθ), (g, polinomiale a tratti costruita sugli elementi della sezione dell'elemento di rivoluzione), dunque per una sollecitazione di tipo trilobata, si avrà sempre una risposta di tipo trilobata e mai quadrilobata etc..
 Nel complesso, considerando un generico caricamento, è consentito, scomporre mediante serie di Fourier, le varie armoniche di sollecitazione, risolverle singolarmente e sommare in fine i singoli risultati, con l'ipotesi di linearità.
Nel complesso, considerando un generico caricamento, è consentito, scomporre mediante serie di Fourier, le varie armoniche di sollecitazione, risolverle singolarmente e sommare in fine i singoli risultati, con l'ipotesi di linearità.
Caricamento elastoplastico
Lo stato tensionale di una struttura non risulta definito, esclusivamente dal carico istantaneo, ma sarà necessario conoscere la storia del caricamento, potranno infatti sussistere condizioni a pari caricamento generanti tuttavia differenti allungamenti plastici εp. Ad ogni caricamento, corrispondono due componenti di allungamento, una elastica ed una plastica, la prima al rilascio del carico, verrà completamente recuperata dal materiale, la seconda, contrariamente, genererà un allungamento residuo, dovuto appunto alla parzale plasticizzazione dell'elemento. Serie successive di caricamenti e scaricaemnti, determiano un sommarsi di deformazioni plastiche residue, superiori ad esempio ad un singolo caricamento di pari intensità.
Incrudimento isotropo
Sebbene meno vicino al comportamento reale, questo modello è molto usato per la sua semplicità. Nella fase di scarico si percorre il tratto elastico fino a un punto caratterizzato da un valore simmetrico dello sforzo. Da lì in poi si segue la curva monotonica ribaltata.
Io parto da una funzione di scarico e comincio a caricare, parto dall'origine dei assi fino ad un certo punto Rs , considero un materiale vergine non scaricato. Procedo a caricare in questa condizione poi magari scarico i successivi caricamenti del materiale il valore di snervamento sarà non più Rs ma Rs’ in quanto incrudito per caricamenti successivi vado su Rs che è funzione della storia di carico. Facciamo che io parto da questa condizione, decido di caricare in pressione e non in compressione. Se L’incrudimento e di tipo isotropo a compressione il sistema inizia a snervare a Rs’.
Incrudimento cinematico
Sebbene meno vicino al comportamento reale, questo modello è molto usato per la sua semplicità. Nella fase di scarico si percorre il tratto elastico fino a un punto caratterizzato da un valore simmetrico dello sforzo. Da lì in poi si segue la curva monotonica ribaltata. Tale modello riesce a descrivere l’effetto Bauschinger. Avevo una forchetta dello stato tensionale da +Rs a – Rs e quindi ho un certo 2Rs del materiale elastico snervo in trazione poi incomincio a comprimere ho snervamento in compressione quando a partire da questo punto scendo in Rs e di un altro Rs e riprendo la mia forchetta di un 2Rs. Per snervamento in trazione mi indebolisce il materiale in compressione.
la teoria di Bauschinger
Si definisce effetto Bauschinger (dal nome dell'ingegnere tedesco Johann Bauschinger) il fenomeno di isteresi plasticizzante dei materiali duttili, cui corrisponde un incrudimento di tipo cinematico. Analizzando un materiale duttile sottoponendolo ad una prova uniassiale, è possibile definire un diagramma sforzo-deformazione, che presenterà una fase elastica lineare ed una plastica. Il confine fra le due fasi è segnato da un valore di tensione di snervamento a trazione fy(t), ed uno a compressione fy( c ); supponendo di sottoporre un corpo ad uno stato di sforzo di trazione f'y(t) superiore a questo valore, dal momento in cui il materiale viene soggetto a scarico e successivamente ad una sollecitazione di compressione, la nuova tensione di snervamento a compressione avrà un valore inferiore a fy( c ). Questo fenomeno è giust'appunto l'effetto Bauschinger, che si verifica a causa della traslazione della superficie di plasticizzazione (incrudimento cinematico), verso un punto rappresentativo dello stato di sollecitazione di trazione. Un procedimento analogo si verifica anche invertendo l'ordine di applicazione degli sforzi